Una forma de clasificar las magnitudes fisicas (temperatura, fuerza, masa...) es clasificandolas segun su naturaleza. Existen las magnitudes escalares, que quedan totalmente definidas con un numero (p ej. la masa ), también las magnitudes vectoriales (p ej, la fuerza), que necesitan estar definidas por un vector, y por ultimo las tensoriales (p ej, tensor de tensiones), que se definen con tensores.
Un vector se puede definir de muchas maneras. Es una matriz de orden 1*n o n*1 donde n denota las componentes del vector. Tambien se define como un tensor de orden 1. O graficamente, como una linea con una flecha. Un vector posee una direccion, que es la recta soporte del vector; un punto de aplicacion, que es donde esta aplicado ese vector; un sentido sobre la recta y una intensidad o modulo, que es la longitud del vector y siempre es positivo.
Un vector unitario es aquel que su modulo es uno. Un vector cualquiera se puede expresar como su direccion y sentido (vector unitario en la direccion del vector) multiplicado por su modulo. Para hallar el vector unitario de un vector es tan sencillo como dividir ese vector por su módulo.
El modulo de un vector se halla de la siguiente manera, siendo V = (a,b,c) un vector de 3 componentes cualquieras.
|V| = modulo de V = √( a ² + b ² + c ²)
Un vector que une dos puntos del espacio, se calcula haciendo extremo menos origen, es decir; si yo lo que quiero es unir lso puntos A(2,5,4) y B(4,1,-2) seria de la siguiente forma
AB = (4-2, 5-1, 4+2) = (2, 4, 6)
Un vector en el espacio se suele expresar como la combinacion lineal de tres vectores unitarios entre si, en el sistema cartesiano se denotan como i,j,k y corresponde a las direcciones x,y,z del espacio cartesiano. Un vector de coordenadas (2,4,-1) se puede representar tambien como 2i + 4j - k.
Operaciones con vectores
Las operaciones con vectores se parecen en algunos aspectos a las de los escalares. Antes de nada comentar que es imposible dividir un vector entre otro vector.
- Suma
La suma de un vector V=(a,b,c) con otro U(m,n,p) se hace de la siguiente manera V+U= (a + m, b + n, c + p)
- Diferencia
La diferencia de vectores se realiza analogamente a la de la suma, es decir, restando componente a componente.
- Producto de un vector por un escalar
Si queremos multiplicar un vector por un escalar lo realizariamos de la siguiente manera. Sea V=(a,b,c) un vector de 3 componentes y sea J un escalar cualquiera entonces:
J * V = J* (a, b, c) = (J*a, J*b, J*c)
La division por un escalar no es mas que el producto por una fracción, asi que se realiza del mismo modo.
- Producto escalar de dos vectores:
El producto escalar de dos vectores es una operación que convierte dos vectores en un escalar. El producto escalar se utiliza asiduamente para calcular el angulo entre dos vectores. Sean V= (a, b, c) y U ( m, n, p) dos vectores cualesquiera, y sea α el angulo que forman. Su producto escalar es:
V * U = |V| * |U| * cos(α) = a*m + b*n + c*p
Se demuestra rapidamente que si el angulo que forman dos vectores es 90º, el producto escalar de esos vectores sera nulo.
- Producto Vectorial de dos vectores:
El producto vectorial de dos vectores es una operacion que transforma dos vectores en uno ortogonal a los dos anteriores. Asimismo, geometricamente el modulo del producto vectorial de dos vectores es el area del paralelogramo que forman ellos mismos y otros dos vectores paralelos a si mismos desde los extremos de los anteriores. Se calcula de la sigueinte manera, con la notacion anterior:
V x U = |U| * |V| * sen(α)
Donde la x es el simbolo del producto vectorial (existe otra notacion tambien). Se demuestra de nuevo facilmente que si los dos vectores son paralelos, es decir, forman 0º, el producto vectorial será nulo.Si la base en la que trabajamos es ortonormal, como por ejemplo, la cartesiana, tambien se puede calcular realizando el determinante siguient:
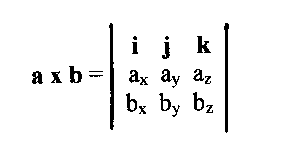Donde a y b son dos vectores cualesquiera. La primera fila del determinante denota la base en la que trabajamos, en este caso la cartesiana, mientras que las 2 lineas inferiores son las componentes de los vectores a y b-Producto mixto de 3 vectores
El producto mixto de 3 vectores da como resultado un escalar. Geometricamente es el volumen del paralelepipedo que formarian eses 3 vectores, y se puede calcular como:
[U,V,W] = producto mixto de U, V y W = U * (V x W)
Donde U, V y W son 3 vectores cualesquiera. Se calcula mas rapidamente como el determinante de la matriz que forman los 3 vectores dispuestos en filas o en columnas. ( si son de 3 componentes) .
Para los que ya sabiais todo esto, un repasillo, para los que no lo sabiais, espero haber conseguido que os entretuvierais ademas de aprender!
Un saludete
No hay comentarios:
Publicar un comentario