Derivada de una función

Hoy hablare sobre la derivada de una funcion, de la que ya comente algo en mi primera entrada del blog.

El calculo diferencial ( y integral) fue desarrollado en sus inicios por Newton y Liebnizt, simualtaneamente pero de forma separada. Como Newton usaba una notacion muy complicada la que ha perdurado hasta nosotros es la de Liebnizt. Basicamente, aqui explicare la necesidad de la derivada, no los metodos para calcularla, si no sus implicaciones mas inmediatas

Imaginemos una recta. Por ejemplo la recta de ecuacion y = x. Es decir, una recta que pasa por el origen de coordenadas y tiene este aspecto



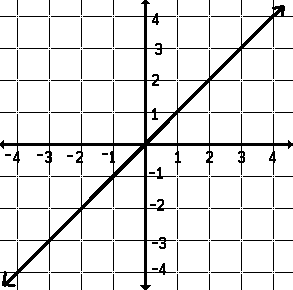
 Imaginemos también que es ladera de una montaña y queremos calcular la pendiente en su base, el punto (0,0) por ejemplo. Para ello tomamos otro punto, por ejemplo el (1,1). La distancia horizontal entre esos dos puntos es 1, al igual que su distancia vertical, por lo tanto:

  Pendiente = lo que sube / lo que avanza horizontalmente = (1 - 0) / (1 - 0) = 1

Era un problema trivial, ya que en la ecuacion de una recta en el plano xy, el numero que multiplica a la x ( el 1 en este caso) es la pendiente y es constante, precisamente por ser una recta.


Pero ahora avanzaremos mas. Supongamos que queremos calcular la pendiente de esta curva de la figura a la que llamaremos F(x), en el punto M. Para ello seguimos el procedimiento anterior, y escojemos un punto, P, de la curva y hallamos la pendiente del mismo modo que antes.


Como se ve en la grafica esta aproximacion a la curva por una recta que une dos puntos no es muy buena, ya que la pendiente de esa recta no va a coincidir con la de la curva en ese punto. Lo que tambien podemos observar, esque la precision aumenta cuanto mas juntos esten los puntos M y P. Llamemos a la distancia entre M y P Δx, como en la figura y llamemos f(x) a la coordenada Y de M; y f(x + Δx) a la coordenada Y de P. Si utilizamos la anterior formula de la pendiente obtenemos:

 Pendiente = lo que sube / lo que avanza horizontalmente =[ f(x+Δx) - f(x) ]/ Δx

Entonces, si llevamos esa distancia Δx cada vez a que sea un numero mas pequeño, moviendo el punto P sobre la curva hasta que esten lo mas cerca posible, es decir haciendo el limite de la pendiente cuando Δx tiende a 0, llegariamos a la seguiente expresion.

Pendiente = f ' (x) = lim    [ f(x + Δx) - f(x)] / Δx

                                Δx->0

Eso es precisamente la derivada de la función F(x) o f ' (x). La derivada se puede definir tambien como la pendiente de la recta tangente a la curva a estudio en el punto eligido, o; como en el caso actual, al ser f(x), en un punto genérico x. Gracias a la derivada, podemos evaluar cambios en las magnitudes que se producen gradualmente ( ver http://brevesrelatosdelaciencia.blogspot.com/2011/10/breve-y-amena-introduccion- al-calculo.html ). La derivada es una herramienta matématica clave y la base del cálculo infinitesimal, sin la cual la mayoria de los objetos tecnologicos de los que disponemos nunca podrian haber sido diseñados; asique le debemos mucho a Newton y a Liebnitz.

A partir de esta entrada se me ha ocurrido proponer algun ejercicio para que el que este interesado que lo realice y exponga su solucion, o pregunte cualquier duda, en un comentario o un email. Ahi va uno:

Calculese la derivada de las siguientes funciones:


- y = f(x) = x⁴ + 3x²
- y = f(x) = cosx + senx
- y = f(x) = 1/ x       para todo x distinto de 0



Saludos!