Correspondencias
La definición formal de correspondencia consiste en que una correspondencia entre dos conjuntos A y B es un subconjunto F del producto cartesiano AxB (explicare lo que es el producto cartesiano en otra ocasión). Para que todos nos entendamos, una correspondencia asigna a determinados elementos del conjunto A una serie de elementos en el conjunto B y ese subconjunto F estará formado por los pares (a,b), estando a contenido en A y b contenido en B.
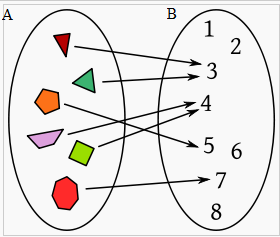 | |||
| Diagrama que intenta representar una correspondencia entre A y B |
- Al conjunto A se le llama conjunto inicial
- Al conjunto B se le llama conjunto final
- Si una pareja de elementos a y b están en la correspondencia se dice que b es una imagen de a y que a es un origen de b
- Llamamos conjunto origen o dominio de F a todos los orígenes de los elementos de B, de forma rigurosa:
Conjunto origen de F= { a∈A / ∃y ∈ B con (a,y) ∈ F}
- Llamamos conjunto imagen o recorrido de F al conjunto formado por todas las imágenes de los elementos de A, de forma rigurosa:
Conjunto imagen de F= { b∈B / ∃x ∈ A con (x,b) ∈ F}
Analizando el caso de la figura como ejemplo tenemos:
- El conjunto A o inicial es:
A={Triángulo rojo(TR),Triángulo verde (TV),Pentágono naranja (PN),Romboide morado (RM),Cuadrado verde (CV), Heptágono rojo (HR)}
- El conjunto B o final es:
B={1,2,3,4,5,6,7,8}
- El subconjunto F o correspondencia es:
F={ ( TR,3); (TV,3); (PN,5); (RM,4); (CV,4); (HR,7) }
- El conjunto origen es:
Conjunto origen = {TR,TV,PN,RM,CV,HR}
- El conjunto imagen es:
Conjunto imagen = {3,4,5,7}
Una vez hemos comentado la definición y aspectos más importantes de las correspondencias, explicaremos un tipo concreto de ellas que son las aplicaciones.
Aplicaciones
Una aplicación entre dos conjuntos A y B es una correspondencia que verifica las siguientes condiciones:
- El conjunto inicial coincide con el conjunto origen, de forma rigurosa:
∀a∈ A, ∃b∈ B / (a,b) ∈ F
- Cada elemento del conjunto origen tiene una única imagen (∃* significa "existe solo uno")
∀a∈C.Origen, ∃*b∈ B / (a,b) ∈ F
 |
| Figura que representa una aplicación de dos conjuntos X e Y |
Se suele denotar una aplicación F de A en B por
f: A -------> B
Cuando la pareja de valores (a,b)∈F, con a ∈ A y b∈B, entonces escribimos:
f(a)=b
Si os dais cuenta, la manera de escribir f(a)=b es idéntica a la notación que usábamos con las funciones, y eso nos lleva a algo muy importante, las funciones son la misma cosa que las aplicaciones. Cuando manejamos una función y=y(x), los valores de x son el conjunto origen y los valores de y el conjunto imagen.
Clasificaremos las aplicaciones (o funciones) en 3 categorías en función de que cumplan o no una serie de características:
- Una aplicación inyectiva es aquella que cada elemento de la imagen tiene un único origen. De forma rigurosa:
f es inyectiva ⇔ f(x) = f(y) ⇒ x = y
 |
| Ejemplo de aplicación inyectiva |
- Una aplicación sobreyectiva es aquella en la que el conjunto imagen coincide con el final:
f es sobreyectiva ⇔ f(A) = B ⇔ ∀b∈B, ∃a∈A / f(a) = b
 |
| Aplicación sobreyectiva |
- Y para terminar, una aplicación es biyectiva si es a la vez inyectiva y sobreyectiva; es decir:
f es biyectiva ⇔ ∀b∈B, ∃*a∈A / f(a) = b
 |
| Aplicación biyectiva |
Esta clasificación de las funciones es de gran importancia, ya que la inyectividad, sobreyectividad y sobretodo la biyectividad son condiciones necesarias para que se cumplan determinados teoremas del cálculo y el análisis matemático.
Y esto es todo sobre correspondencia y aplicaciones. Es simplemente un esbozo acerca de estos temas, pero el concepto importante sobre ambas es que una correspondencia es simplemente la asignación de un miembro de un conjunto a otro miembro de otro conjunto sin ninguna especificación; mientras que las aplicaciones, que son otra forma de llamar a las funciones, los relacionan respetando unas determinadas condiciones.
Hasta otra amigos!





.jpg)