Lo basico de las funciones reales de variable real

Hola amigos! La proxima entrada es posible que ya aborde temas fisicos aplicados. Hoy hablare de las funciones. Ya las introduje en las entradas sobre calculo, pero en ellas estaba suponiendo que la gente sabia muchas cosas que quizas no sabe, o que quizas convenga repasar. Alla vamos


Una funcion real de variable real es la relacion entre una variable independiente ( normalmente "x") y una variable dependiente ( normalmente "y"). Son variables porque no son valores constantes, como un numero, si no que la "y" varia segun como varia la "x" ("y" varia en funcion de "x"). las funciones son algo inherente en la naturaleza. Se utilizan en todos los campos en los que la matematica tiene alguna importancia. Las relaciones entre dos fenomenos (Velocidad y espacio recorrido, Oferta y demanda....) se suelen modelizar como funciones. Si una variable "y" depende de otra "x", se suele escribir de esta manera para mostrar su dependencia  y (x). Para calcular el valor de y que tiene una x dada se introduciria el valor de x en la ecuacion de la funcion y se obtendria el valor de y como si de una ecuacion normal se tratase. Se suelen representar en dos ejes coordenados: El eje de abscisas, en el que se situa la x, y el eje de ordenadas en el que se situa la y. Una forma facil de representar funciones en el plano es construir una tabla de valores, ir situando los puntos en un plano y luego unirlos como es debido.

Las funciones se clasifican de muchas formas. Una forma es por ejemplo diferenciar entre funciones linales y no lineales. Las funciones lineales son rectas y siempre tienen la misma expresion:

     y (x) = mx + n

Donde m es la pendiente de la recta, es decir la relacion entre lo que avanza verticalmente y lo que avanza horizontalmente y n es la "ordenada en el origen" ( es decir, cuando la x es igual a 0 el valor que toma la y). Esta es la forma que toma, por ejemplo, la funcion y = 2x - 3

Las funciones no lineales pueden ser de muchos tipos ( Parabolicas, Hiperbolicas, Senoidales...). basicamente son todas aquellas en las que la funcion no es de la forma   y = mx + n

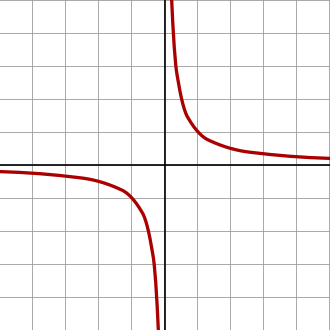
Otro tipo de separacion es la que existe entre funciones continuas y no continuas. Para no entrar en asuntos de limites y continuidad de funciones. Una funcion discuntinua es aquella que la dibujarla no es una linea continua si no que tiene saltos, ausencia o desplazamiento de puntos o ramas que se van al infnito. Un ejemplo de ramas al infinito de una funcion discontinua es la funcion     y = 1/x

Del estudio de las funciones emergen posteriormente todo el edificio del calculo diferencial y integral. Sin duda el analisis de las funciones es una de las partes mas amplias, importantes y complicadas de la matematica. Para terminar os dejo un par de imagenes de funciones habituales y algun que otro ejercicio:

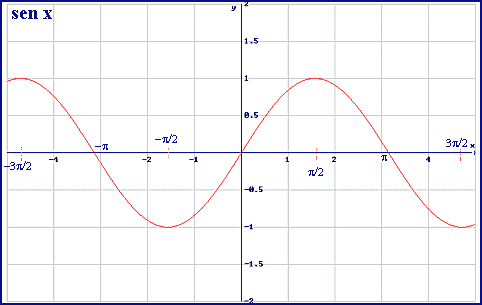
y = sen (x)

y = x ²

Ahora los ejercicios:

- Calcular el valor de las funciones siguientes en los puntos que se piden

 y = 2x² +12         en   x = 12

 y = sen ( x² / 2)    en    x = 6

y  = 1 / ( x-1 )       en    x = 1

Trigonometria Basica

Despues de la resaca de año nuevo vuelvo con fuerzas para daros unas nociones de trigonometria basica, y para los que la estudieis, las claves para que no se atasque demasiado.



Aunque en la trigonometria hay muchas formulas, realmente solo es necesario saber utilizar unas cuantas muy basicas. Para empezar diremos que la trigonometria es la rama de las matematicas que se ocupa de las "cosas que les pasan a los triangulos" , concretamente se centra en los triangulos rectangulos (aquellos que tienen un angulo recto, es decir, que forma 90º).

En un triangulo rectangulo pasan muchas cosas interesantes. Para empezar, el teorema de Pitagoras, conocido por todo el mundo, pero que es muy importante en trigonometria. Ahora vamos con los senos, cosenos y tangentes de los angulos.

El Seno de un ángulo se define como el cociente entre el cateto opuesto al angulo de estudio y la hipotenusa: Si quisieramos calcular el Seno del angulo que forman los lados rojo y verde del triangulo, (llamemos a ese angulo α) entonces procederiamos asi:

   Sen α = y / h

El Coseno de un ángulo se define a su vez como el cociente entre el cateto contiguo al angulo de estudio y la hipotenusa. Si seguimos con el angulo anterior, el coseno de α sera entonces: 

Cos α = x / h

La ultima de estas definiciones es la de la tangente. La Tangente de un ángulo es el cociente entre el cateto opuesto al angulo y el cateto contiguo. La tangente de α es igual a:

Tan α = tg α = y / x = sen α / cos α

La tangente de un angulo tambien es la relacion entre el seno y el coseno de ese angulo.

En trigonometria existen multitud de relaciones entre senos cosenos y tangentes. Pero con 4 de ellas se puede definir al resto:

1º)       Cos² α + Sen² α = 1   → Demostrado en la entrada 2 del blog ( http://brevesrelatosdelaciencia.blogspot.com/2011/10/introduccion-las-demostraciones.html )

2º)       Sen ( α + β ) = Sen (α) * Cos (β) + Sen (β) * Cos (α)

3º)      Cos ( α + β) = Sen(α) * Sen(β) + Cos(β) * Sen(α)

4º)      1 + tg² α =   1 / cos² α

Siendo α y β dos angulos cualesquiera

Con estas 4 ecuaciones se convierte en innecesario saberse de memoria las ecuaciones del angulo doble y del angulo mitad, porque son todas deducibles a partir de estas. Y esque es importante recordar que en las matematicas, es mucho mas facil usar la logica que recordar formulas infumables.


Como casi todas las operaciones matematicas, el seno, el coseno , y la tangente tienen operaciones inversas. El arcoseno de un valor dado transforma ese valor dado en el angulo cuyo seno coincidiria con ese valor.  El arcocoseno y el arcotangente funcionan de la misma manera pero para el coseno y la tangente respectivamente. 

Las funciones trigonometricas son fundamentales en la fisica y en las matematicas. El Seno, el Coseno y la tangente son funciones periodicas que definen los comportamientos de muchos fenomenos fisicos y, para no aburrir, son la forma mas rapida de relacionar distancias con angulos.

Hasta otra amigos!